Curvas Cónicas

8.1. Curvas cónicas

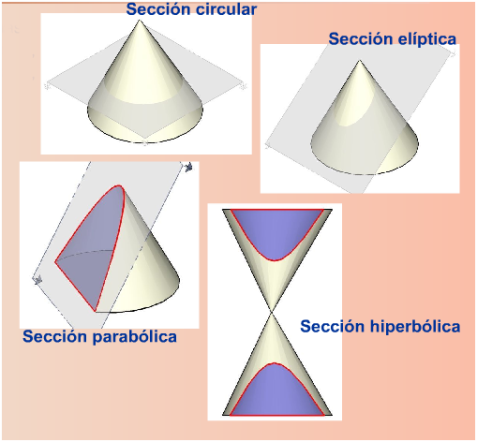
Como se ha dicho en el capítulo anterior, las curvas geométricas son aquellas que se pueden construir por medio de arcos, trazados con el compás, y por medio de puntos. Las curvas cónicas forman parte de las curvas geométricas.

Curvas cónicas son las que surgen a partir de las secciones producidas por un plano, cuando corta la superficie de un cono recto. Tipos de secciones:

• Sección circular
• Sección elíptica
• Sección parabólica
• Sección hiperbólica

Desarrollo

---

8.1.1. Sección circular

El plano de corte es perpendicular al eje del cono. La curva geométrica que se obtiene a partir de esta sección es: la circunferencia.


La circunferencia

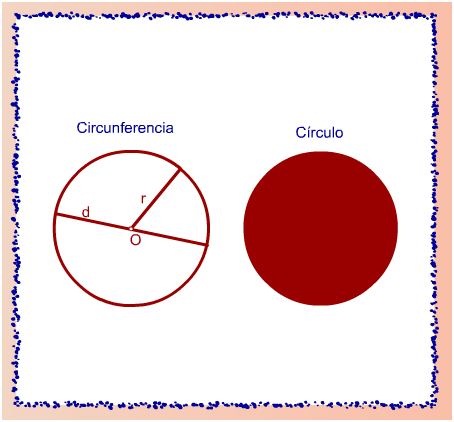
Es la curva cerrada y plana formada por puntos que equidistan de otro punto O llamado centro.

Radio. Es cualquier segmento (r) que tiene un extremo en el centro de la circunferencia y el otro sobre ella.

Diámetro. Es el segmento (d) que une dos puntos de la circunferencia alineados con el centro.

Círculo. Es la superficie comprendida dentro de la circunferencia.

8.1.2. Sección elíptica

El plano de corte forma un ángulo oblicuo, con el eje del cono, sin llegar a ser paralelo a ninguna generatriz del cono. La curva geométrica que se obtiene a partir de esta sección es: la elipse.


La elipse
Es una curva cerrada y plana formada por puntos que tienen la propiedad de que la suma de las distancias de cada uno de ellos a otros dos fijos, llamados focos, es constante e igual al eje mayor de la elipse. En todos los puntos de la elipse (por ejemplo el Q2) se cumple:

r + r’ = AB

8.1.3. Sección parabólica

Surge cuando el plano de corte es paralelo a una de las generatrices del cono. La curva geométrica que se obtiene a partir de esta sección es: la parábola.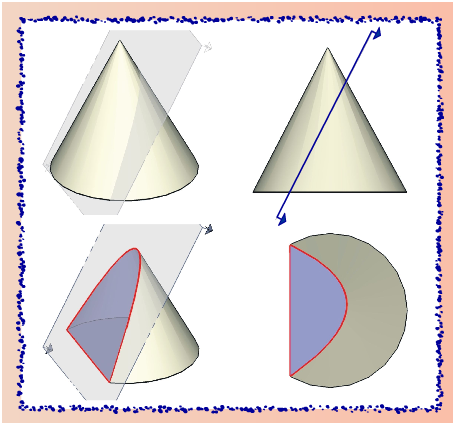


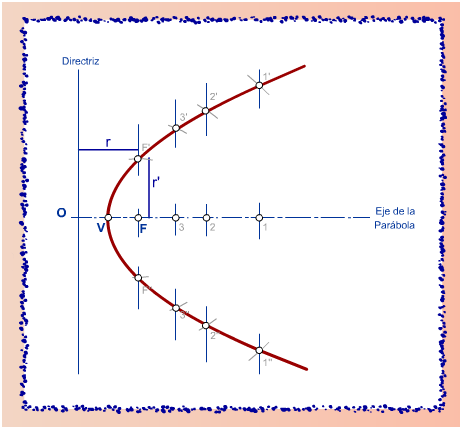
La parábola
Es una curva plana, formada por puntos que tienen la propiedad de estar cada uno de ellos equidistante de un punto fijo, llamado foco, y de una recta llamada directriz. En todos los puntos de la curva, por ejemplo el punto F’, se cumple que r = r’ El vértice V es el punto medio de OF, distancia existente entre el foco y la directriz

8.1.4. Sección hiperbólica

El plano de corte es paralelo al eje del cono y corta dos conos, opuestos por el vértice y con el mismo eje. La curva geométrica que se obtiene a partir de esta sección es: la hipérbola.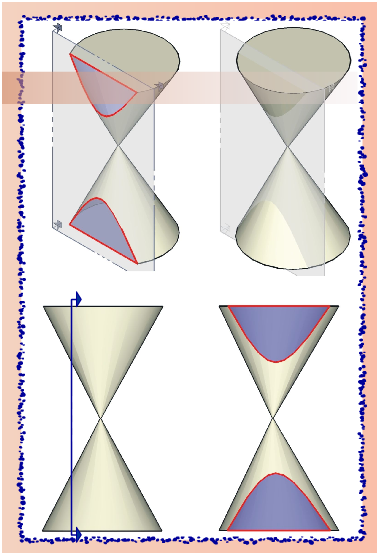



La Hipérbola
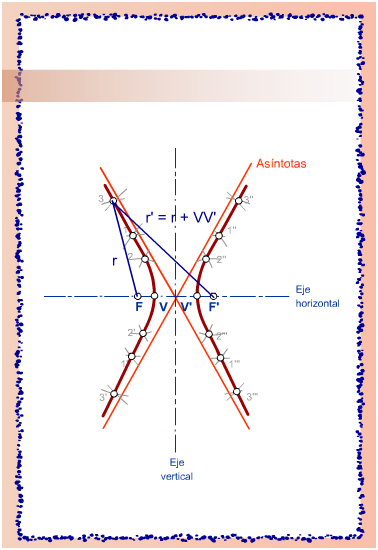
Es una curva abierta y plana formada por puntos, cuya diferencia de distancias a dos puntos fijos de un plano, llamados focos, es constante. Por tanto se cumple que r – r’ = VV’ Asíntotas Son las rectas tangentes a la curva en el infinito.
















http://ibiguri.wordpress.com/cur/8-1/